Another branch of machine learning that has proven its mettle in recent years is recommender systems – systems that recommend products or services to customers. Amazon’s recommender system reportedly drives 35% of its sales. The good news is that you don’t have to be Amazon to benefit from a recommender system, nor do you have to have Amazon’s resources to build one. They’re relatively simple to create once you learn a few basic principles.
Recommender systems come in many forms. Popularity based systems present options to customers based on what products and services are popular at the time – for example, “Here are this week’s bestsellers.” Collaborative systems make recommendations based on what others have selected, as in “People who bought this book also bought these books.” Neither of these types of systems requires machine learning.
Content-based systems, by contrast, typically benefit from machine learning. An example of a content-based system is one that says “if you bought this book, you might like these books also.” These systems require a means for quantifying similarity between items. If you like the movie Die Hard, you might or might not like Monty Python and the Holy Grail. If you like Toy Story, there‘s a good chance you’ll like A Bug’s Life, too. But how do you make that determination algorithmically?
Content-based recommenders require two ingredients: a way to vectorize – convert to 1s and 0s – the attributes that characterize a service or product, and a means for calculating similarity between the resulting vectors. The first one is easy. In my posts on sentiment analysis and spam filtering, you learned about Scikit-learn’s CountVectorizer class and its ability to convert the text in movie reviews and e-mails into tables of word counts. All you need is a way to measure similarity between rows of word counts and you can build a recommender system. And one of the simplest and most effective ways to do that is a technique called cosine similarity.
Cosine Similarity
Cosine similarity is a mathematical means for computing the similarity between pairs of vectors (or data points treated as vectors). The basic idea is to take each value in a sample – for example, word counts in a row of vectorized text – and use them as the endpoint coordinates of a vector. Do that for two samples, and then compute the cosine between vectors in m-dimensional space, where m is the number of values in each sample. Because the cosine of 0o is 1, two identical vectors will have a similarity of 1. The more dissimilar the vectors, the closer the cosine will be to 0.
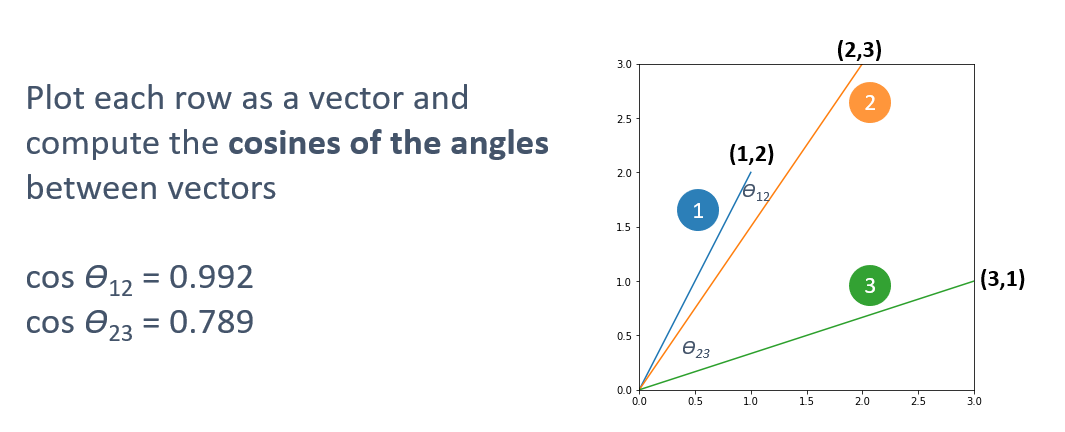
Here’s an example in 2-dimensional space to illustrate. Suppose you have three rows containing two values each:
| 1 | 2 |
| 2 | 3 |
| 3 | 1 |
You want to determine whether row 2 is more similar to row 1 or row 3. It’s hard to tell just by looking at the numbers, and in real life, there are many more numbers. If you simply added the numbers in each row and compared the sums, you would conclude that row 2 is more similar to row 3. But what if you treated each row as a vector?
- Row 1: (0, 0) → (1, 2)
- Row 2: (0, 0) → (2, 3)
- Row 3: (0, 0) → (3, 1)
Now you can compute the cosines of the angles formed by 1 and 2 and 2 and 3 and determine that row 2 is more like row 1 than row 3. That’s cosine similarity in a nutshell.
Cosine similarity isn’t limited to two dimensions; it works in high-dimensional space as well. To help you compute cosine similarities regardless of the number of dimensions, Scikit offers the cosine_similarity function. The following code computes the cosine similarities of the three samples in the example above:
data = [[1, 2], [2, 3], [3, 1]] cosine_similarity(data)
The return value is a similarity matrix containing the cosines of every vector pair. The width and height of the matrix equals the number of samples:

From this, we can see that the similarity of rows 1 and 2 is 0.992, while the similarity of rows 2 and 3 is 0.789. In other words, row 2 is more similar to row 1 than it is to row 3. There is also more similarity between rows 2 and 3 (0.789) than there is between rows 1 and 3 (0.707).
Build a Movie-Recommendation System
Let’s put cosine similarity to work building a content-based recommender system for movies. Start by downloading the dataset, which is one of several movie datasets available from Kaggle.com. This one has information for about 4,800 movies, including title, budget, genres, keywords, cast, and more. Then load the dataset and peruse its contents:
import pandas as pd
df = pd.read_csv('Data/movies.csv')
df.head()
Use the following statements to extract the columns used to judge movies for similarity and fill missing values with empty strings:
df = df[['title', 'genres', 'keywords', 'cast', 'director']]
df = df.fillna('') # Fill missing values with empty strings
df.head()
Next, add a new column named “features” that combines all the words in the other columns:
df['features'] = df['title'] + ' ' + df['genres'] + ' ' + df['keywords'] + ' ' + df['cast'] + ' ' + df['director']
Use CountVectorizer to vectorize the text in the “features” column:
from sklearn.feature_extraction.text import CountVectorizer vectorizer = CountVectorizer(stop_words='english', min_df=20) word_matrix = vectorizer.fit_transform(df['features']) word_matrix.shape
The table of word counts contains 4,803 rows – one for each movie – and 918 columns. The next task is to compute cosine similarities for each row pair:
from sklearn.metrics.pairwise import cosine_similarity sim = cosine_similarity(word_matrix) sim.shape
Ultimately, the goal of this system is to input a movie title and identify the n movies that are most similar to that movie. To that end, define a function named get_recommendations that accepts a movie title, a DataFrame containing information about all the movies, a similarity matrix, and the number of movie titles to return:
def get_recommendations(title, df, sim, count=10):
# Get the row index of the specified title in the DataFrame
index = df.index[df['title'].str.lower() == title.lower()]
# Return an empty list if there is no entry for the specified title
if (len(index) == 0):
return []
# Get the corresponding row in the similarity matrix
similarities = list(enumerate(sim[index[0]]))
# Sort the similarity scores in that row in descending order
recommendations = sorted(similarities, key=lambda x: x[1], reverse=True)
# Get the top n recommendations, ignoring the first entry in the list since
# it corresponds to the title itself (and thus has a similarity of 1.0)
top_recs = recommendations[1:count + 1]
# Generate a list of titles from the indexes in top_recs
titles = []
for i in range(len(top_recs)):
title = df.iloc[top_recs[i][0]]['title']
titles.append(title)
return titles
Essentially, this function sorts the cosine similarities in descending order to identify the count movies most like the one identified by the title parameter. Then it returns the titles of those movies.
Now comes the fun part: using the get_recommendations function to search the database for similar movies. First ask for the 10 movies that are most similar to the James Bond thriller “Skyfall:”
get_recommendations('Skyfall', df, sim)

Now call get_recommendations again to discover movies that are like “Mulan:”
get_recommendations('Mulan', df, sim)
Feel free to try other movies as well. Note that you can only input titles that are in the dataset. Use the following statements to print a complete list of movie titles:
pd.set_option('display.max_rows', None)
print(df['title'])
I think you’ll agree that the system does a pretty credible job of picking similar movies. Not bad for about 20 lines of code!
Get the Code
You can download a Jupyter notebook containing the movie-recommendations example from the machine-learning repo that I maintain on GitHub. Feel free to check out the other notebooks in the repo while you’re at it. Also be sure to check back from time to time because I am constantly uploading new samples and updating existing ones.