My previous post described how to build a neural network that serves as a binary classifier. Here’s a binary classifier that accepts two inputs, has a hidden layer with 128 neurons, and outputs a value from 0.0 to 1.0 representing the probability that the input belongs to the positive class:
model = Sequential() model.add(Dense(128, activation='relu', input_dim=2)) model.add(Dense(1, activation='sigmoid')) model.compile(optimizer='adam', loss=' binary_crossentropy', metrics=['accuracy'])
Key elements include an output layer with one neuron assigned the sigmoid activation function, and binary_crossentropy as the loss function. Three simple modifications repurpose this network to do multiclass classification:
model = Sequential() model.add(Dense(128, activation='relu', input_dim=2)) model.add(Dense(4, activation='softmax')) model.compile(optimizer='adam', loss=' categorical_crossentropy', metrics=['accuracy'])
The changes are as follows:
- The output layer contains one neuron per class rather than just one neuron. If the dataset contains four classes, then the output layer has four neurons. If the dataset contains 10 classes, then the output layer has 10 neurons. Each neuron corresponds to one class.
- The output layer uses the softmax activation function rather than the sigmoid activation function. Each neuron in the output layer yields a probability for the corresponding class, and thanks to the softmax function, the sum of all the probabilities is 1.0.
- The loss function is categorical_crossentropy. During training, categorical cross-entropy exponentially penalizes error in the probabilities predicted by a multiclass classifier, just as binary_crossentropy does for binary classifiers.
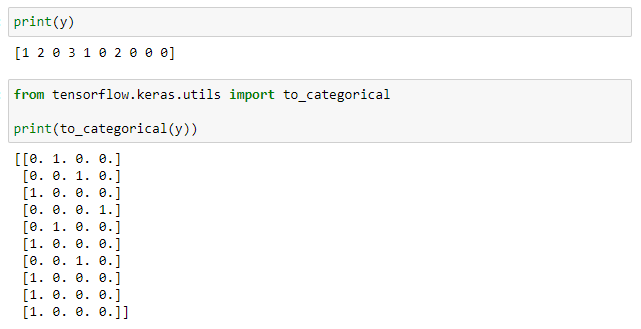
After defining the network, you call fit to train it and predict to make predictions. But there is one nuance. Before training the network, you must one-hot-encode the labels. (For a review of one-hot-encoding, refer to my earlier post on binary classification.) Let’s say the dataset contains four classes. Rather than pass fit a label column containing values from 0 to 3, you pass it four columns containing 0s and 1s. Keras provides a utility function named to_categorical for just that purpose. Here’s a column containing 10 labels representing four classes before and after one-hot-encoding:
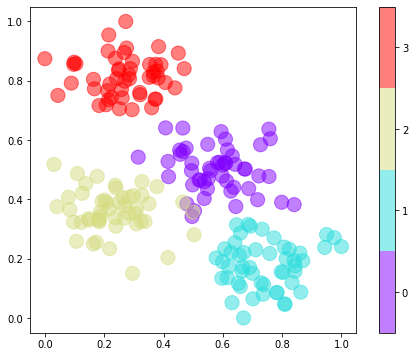
Since an example is worth a thousand words, let’s fit a neural network to a 2-dimensional dataset comprising four classes:
The following code trains a neural network to predict a class based on a point’s x and y coordinates:
model = Sequential() model.add(Dense(128, activation='relu', input_dim=2)) model.add(Dense(4, activation='softmax')) model.compile(optimizer='adam', loss=' categorical_crossentropy', metrics=['accuracy']) hist = model.fit(x, to_categorical(y), epochs=40, batch_size=10, validation_split=0.2)
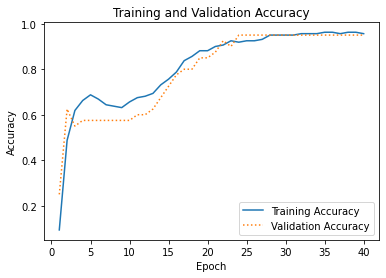
A plot of the training and validation accuracy reveals that the network had little trouble separating the classes:
You make predictions by calling the classifier’s predict method. For each input, predict returns an array of probabilities – one per class. Thanks to the softmax activation function, all the probabilities add up to 1.0. In this example, purple data points represent class 0, light blue represents class 1, taupe represents class 2, and red represents class 3. Here, the network is asked to classify a point that lies at (0.2, 0.8):
model.predict(np.array([[0.2, 0.8]]))
The answer is an array of four probabilities corresponding to class 0, 1, 2, and 3, in that order:
[2.1877741e-02, 5.3804164e-05, 5.0240371e-02, 9.2782807e-01]
The network predicted there’s a 2% chance that (0.2, 0.8) corresponds to class 0, a 0% chance that it corresponds to class 1, a 5% chance that it corresponds to class 2, and a 93% chance that it corresponds to class 3. Looking at the plot, that seems like a reasonable answer.
If you simply want to know which class the point belongs to, you can do it this way:
np.argmax(model.predict(np.array([[0.2, 0.8]])), axis=1)
The answer is 3, which corresponds to red. Older versions of Keras included a predict_classes method that did the same without the call to argmax, but that method has since been deprecated and removed.
Train a Neural Network to Perform Facial Recognition
My post on support-vector machines documented the steps for training an SVM to recognize faces. Let’s train a neural network to do the same. We’ll use the same dataset as before: the Labeled Faces in the Wild dataset, which contains more than 13,000 facial images of famous people and is built into Scikit as a sample dataset. Of the more than 5,000 people represented in the dataset, 1,680 have two or more facial images, while only five have 100 or more. We’ll set the minimum number of faces per person to 100, which means that five sets of faces corresponding to five famous people will be imported. Each facial image is labeled with the name of the person that the face belongs to.

Start by creating a new Jupyter notebook and using the following statements to load the dataset:
import numpy as np import pandas as pd from sklearn.datasets import fetch_lfw_people faces = fetch_lfw_people(min_faces_per_person=100) image_count = faces.images.shape[0] image_height = faces.images.shape[1] image_width = faces.images.shape[2] class_count = len(faces.target_names) faces = fetch_lfw_people(min_faces_per_person=100) print(faces.target_names) print(faces.images.shape)
In total, 1,140 facial images were loaded. Each measures 47 by 62 pixels. Use the following code to show the first 24 images in the dataset and the people to whom the faces belong:
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
fig, ax = plt.subplots(3, 8, figsize=(18, 10))
for i, axi in enumerate(ax.flat):
axi.imshow(faces.images[i], cmap='gist_gray')
axi.set(xticks=[], yticks=[], xlabel=faces.target_names[faces.target[i]])
Check the balance in the dataset by generating a histogram showing how many facial images were imported for each person:
from collections import Counter
counts = Counter(faces.target)
names = {}
for key in counts.keys():
names[faces.target_names[key]] = counts[key]
df = pd.DataFrame.from_dict(names, orient='index')
df.plot(kind='bar')
There are far more images of George W. Bush than of anyone else in the dataset. Classification models are best trained with balanced datasets. Use the following code to reduce the dataset to 100 images of each person:
mask = np.zeros(faces.target.shape, dtype=np.bool)
for target in np.unique(faces.target):
mask[np.where(faces.target == target)[0][:100]] = 1
x_faces = faces.data[mask]
y_faces = faces.target[mask]
x_faces.shape
x_faces contains 500 facial images, and y_faces contains the labels that go with them: 0 for Colin Powell, 1 for Donald Rumsfeld, and so on.
The next step is to normalize pixel values by dividing them by 255, and convert the target values (the 0-based indices identifying the person to whom a face belongs) into categorical values by one-hot-encoding them. After that, split the data for training and testing. As we did in the previous post, we’ll set aside 20% of the data for testing, let Keras use it to validate the model during training, and later use it to assess the results using a confusion matrix:
from tensorflow.keras.utils import to_categorical
from sklearn.model_selection import train_test_split
face_images = x_faces / 255
face_labels = to_categorical(y_faces)
x_train, x_test, y_train, y_test = train_test_split(face_images, face_labels, train_size=0.8, stratify=face_labels, random_state=0)
Create a neural network containing one hidden layer with 512 neurons. Use categorical_crossentropy as the loss function and softmax as the activation function in the output layer since this is a multiclass classification task:
from keras.layers import Dense from keras.models import Sequential model = Sequential() model.add(Dense(512, activation='relu', input_shape=(image_width * image_height,))) model.add(Dense(class_count, activation='softmax')) model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy']) model.summary()
Now train the network:
hist = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=100, batch_size=25)
Use the test data to generate a confusion matrix to visualize how the network performs:
from sklearn.metrics import confusion_matrix
y_predicted = model.predict(x_test)
mat = confusion_matrix(y_test.argmax(axis=1), y_predicted.argmax(axis=1))
sns.heatmap(mat, square=True, annot=True, fmt='d', cbar=False, cmap='Blues',
xticklabels=faces.target_names,
yticklabels=faces.target_names)
plt.xlabel('Predicted label')
plt.ylabel('Actual label')
How many times did the model correctly identify George W. Bush? How many times did it identify him as someone else? Would the network be just as accurate with 128 neurons in the hidden layer as it is with 512?
Get the Code
You can download a Jupyter notebook containing the facial-recognition example from the deep-learning repo that I maintain on GitHub. Feel free to check out the other notebooks in the repo while you’re at it. Also be sure to check back from time to time because I am constantly uploading new samples and updating existing ones.